Kvantitatīvā izglītība
Autors
Par mūsu sabiedrības visai
apšaubāmo kvantitatīvās izglītības līmeni
(ang. quantitative literacy) liecina ciparu vīrusa
plašā izplatība politiķu, žurnālistu,
ierēdņu un pat dažu zinātnieku leksikā. Šķiet,
ka pirmais šo vīrusu apgrozībā palaida Aivars Guntis
Kreituss.
Ciparu vīruss
Tas izrādījās tik virulents, ka tagad
būs grūti atrast žurnālistu vai politiķi, kurš ar
to nebūtu inficēts. Firmu investīciju apjomi tiek ilustrēti
ar cipariem, darba vietu skaits tiek dēvēts par ciparu. Uzņēmuma
peļņa izteikta ar tiem vai citiem cipariem utt. Latviešu valodas
vārds skaitlis tiek padzīts no mūsu leksikas un
aizstāts ar ciparu. Tādēļ nebūs lieki
atgādināt, ka decimālajā skaitīšanas
sistēmā mēs lietojam desmit arābu ciparus 0, 1, 2, 3, 4, 5,
6, 7, 8, 9, bet binārajā tikai divus 0, 1.
Vieni un tie paši cipari dažādā
sakārtojumā apzīmē atšķirīgus skaitļus,
kuru vienādošana vienādo ciparu dēļ ne ar ko nav
attaisnojama. Pavisam smieklīgi skan apgalvojums, ka cipars 521 ir
lielāks par ciparu 125. Tikpat dīvaini skan apgalvojums, ka
zinātnei atvēlētais valsts budžeta cipars 0,2 procenti no
iekšzemes kopprodukta turpmākajos gados jāpaaugstina, lai
sasniegtu 1 procentu.
Mērskaitļu
dīvainības
Gan ikdienā, gan zinātnē
operējam ar kvantitātēm, kuras interpretējamas kā
zināmu lielumu salīdzinājumi ar noteiktiem etaloniem
mērvienībām. Zemes platības tiek izteiktas hektāros
vai kvadrātkilometros, ķermeņa masa gramos, kilogramos vai
tonnās. Elektrisko strāvu spriegumi voltos vai kilovoltos utt. Lai
pareizi operētu ar mērskaitļiem, precīzi jāievēro
etalonu, t. i., izmantoto mērvienību savstarpējās
attiecības. Īpaši uzmanīgam jābūt ar
mērvienībām, kuras nepieder metriskajai sistēmai. Spilgtu
liecību par tulkotāju un redaktoru kvantitatīvās
izglītības līmeni sniedz Žila Verna grāmatā Žangada
sastopamie elektrisko zušu un skudrulāču raksturlielumi. Tur
lasāms, ka elektrisko zušu garums sasniedzot 20 pēdas, platums
8 sprīžus, skudrulāču nagu garums 5 sprīžus.
Rodas jautājums, kādi ir šo
dzīvo būtņu izmēri metriskajās vienībās? Ja
ar pēdu domāta angļu pēda (foot), tad mums būs
darīšana ar gigantiskiem radījumiem, kuru garums
svārstās no 4,5 līdz 6 metriem. Neskaidrs paliek jautājums
par elektrisko zušu platumu un skudrulāču nagu garumu. Franču
mēra sistēmā tāda mērvienība kā sprīdis
nav atrodama, tas pats sakāms par angļu mēriem. Ja ar
sprīdi saprotam pieauguša cilvēka sprīža vidējo
garumu, tad šis etalons nebūs mazāks par 15 cm.
Tātad elektrisko zušu platums nebūs mazāks par 1,2 m, bet
skudrulāča nagu garums sasniegs 75 cm. Jāšaubās, vai
Žils Verns būtu paudis šādas zooloģiskas
aplamības. Tas izskaidrojams ar grāmatas tulkotājas Mirdzas
Ersas kvantitatīvās izglītības trūkumiem.
Par kvantitatīvās izglītības
kuriozu jānosauc grāmatas Atveseļojies pats! sastādītājas
un redaktores T. Laubes rekomendācija kāda ārstnieciska
preparāta sagatavošanai. Lasītājam tiek dots
norādījums izšķīdināt 8 g medus 8 mg ūdens!
Šajā pašā darbā jauktas tādas
mērvienības kā dekalitri un decilitri, lasāmas arī
citas dīvainības.
Ar daudz sarežģītāku
kvantitatīvās izglītības problēmu saduramies
jautājumos, kas attiecas uz sakaru tehnikas un informācijas drošības
jautājumiem. Šeit nereti gadās, ka eksaktas
mērvienības objektīvi nav iespējamas, bet vienlaikus
pastāv nepieciešamība kādas kvantitatīvas noteiksmes
salīdzināt, t. i., tās kaut kādā veidā
mērīt. Spilgts piemērs tam ir elektroniskā paraksta
drošums.
Ja apgalvo, ka Latvijā tiks ieviests
drošs elektroniskais paraksts, tad lasītājam var rasties
iespaids, ka šī paraksta drošība ir kas absolūts.
Faktiski drošs elektroniskais paraksts tomēr ir apveltīts ar noteiktu
nedrošības līmeni, jo tā viltošana (ang. forgery)
tāpat ir iespējama. Tātad rodas jautājums, cik īsti
drošs, resp., nedrošs, būs mūsu elektroniskais paraksts?
Mēs prasām pēc kāda kvantitatīva
rādītāja, kas šo drošības līmeni izteiktu.
Nedaudz vienkāršojot situāciju,
varam teikt, ka drošības kvantitatīvais rādītājs
ir elementāro aritmētisko operāciju skaits, kas
nepieciešams, lai izskaitļotu, t.i., atrastu, nezināma elektroniskā
paraksta atslēgu jeb paraksta veidošanas algoritmu. Ja
nepieciešamo operāciju skaits šāda mērķa
sasniegšanai būtu 1 sekstiljons, t. i., 1021, tad
vismodernākajam datoram būtu jāpatērē vismaz 30 gadi,
lai šo uzdevumu veiktu. Šis aprēķins balstās uz pieņēmumu,
ka šodien tiek konstruēti datori, kuru darbības ātrums
būs triljons aritmētisku operāciju sekundē. Tā kā
sekunžu skaits vienā gadā nav lielāks par 32 miljoniem, tad
gada laikā šāds dators izpildīs 3,2*1019
operācijas. Dalot 1021 ar 3,2*1019, dabūsim
31,25, kas izsaka nepieciešamo gadu skaitu.
Mūsu atbilde tomēr rāda, cik
relatīvs ir šāds augstas drošības
rādītājs. Atliek tikai pacelt datora ātrdarbību par
vienu vai divām kārtām, un drošais elektroniskais paraksts
kļūs ārkārtīgi nedrošs.
Kvantitātes un skaitļi
Mūsu izpratne par kvantitātēm, par
lielumiem primāri balstās uz jēdzienu skaits, kas
abstrahēts no mūsu pieredzes, darbojoties ar viendabīgu
priekšmetu kopām, t. i., skaitot lopus ganāmpulkā,
bērnus ģimenē, zvērādas noliktavā, karotāju
skaitu ciltij utt. Tā nonāca pie jēdziena naturāls
skailtis jeb dabisks skaitlis. Decimālajā
skaitīšanas sistēmā tos pierakstām ar jau
pieminētajiem desmit arābu cipariem, bet binārajā jeb
diviskajā skaitīšanas sistēmā ar cipariem 0 un 1.
Naturālo skaitļu fundamentālo nozīmi ievērojamais
vācu matemātiķis Leopolds Kronekers (1823.1891.) izteica ar
šādu sentenci: - Dievs radīja naturālos skaitļus,
pārējais ir cilvēku roku darbs.
Nākošā pakāpe mūsu
izpratnē par kvantitātēm saistās ar naturālo
skaitļu attiecībām jeb t. s. racionālajiem skaitļiem:
½, 1/3, ¼, 1/5, 2/3, 2/4, 3/5 utt. Grieķi vairākus
gadsimtus pirms mūsu ēras atklāja, ka dažu lielumu izteikšanai
arī racionālie skaitļi ir nepietiekami. Viņi
pierādīja, ka kvadrāta malas attiecība pret tā diagonāli
nav izsakāma ar racionālu skaitli, t. i., ar divu naturālu
skaitļu m un n attiecību m/n. Ja kvadrāta malas garums ir 1m,
tad tā diagonāles garums būs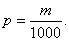 m. Tātad šo divu
nogriežņu garumu attiecība būs
m. Tātad šo divu
nogriežņu garumu attiecība būs 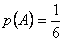 , kur
, kur 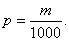 ir irracionāls skaitlis, kas
pierakstāms kā bezgalīga, nepereodiska decimāldaļa.
ir irracionāls skaitlis, kas
pierakstāms kā bezgalīga, nepereodiska decimāldaļa.
Tagad skaitļa jēdziens ar daudzu
matemātiķu pūlēm paplašināts līdz t. s.
kompleksajiem skaitļiem, kuru loma modernajā zinātnē nav
pārvērtējama. Ikdienā cilvēki iztiek ar
naturāliem un racionāliem skaitļiem, pēdējos
visbiežāk pierakstot decimālskaitļu formā. Pēc
lieluma šie skaitļi reti kad pārsniedz miljardu un tikpat reti
to vērtība mazāka par vienu miljardo daļu, t. i,
1/10000000000. Taču pašreizējā ikdiena būtiski
atšķiras no ikdienas pagātnē. Senie grieķi
praktiskās lietas kārtoja tādu kvantitāšu ietvaros,
kuru mērskaitļi atradās robežās starp 1/1000 un 1000;
nulli viņi par skaitli neuzskatīja. Skaitli 10 000 grieķi
apzīmēja ar vārdu miriāde. Tas viņiem
šķita tik milzīgs, ka drīz vien ar to apzīmēja
kaut ko neskaitāmu. Tā, piemēram, sāka runāt par
zvaigžņu miriādēm, par kukaiņu miriādēm u. tml.
Arī senajā Krievzemē, runājot par skaitu, kas izsakāms
ar 10 000, lietoja izteiksmīgu vārdu tumsa (kr. ņüģą). Bet
jau 17. gs. ņüģą apzīmēja miljonu. Tehnoloģijas
attīstība cilvēkus spiež arī ikdienā lietot
arvien lielākus un lielākus skaitļus. Mūsdienu
jaunieši jau runā par diskiem, kuru kapacitāte izsakāma
gigabaitos, t. i., miljardos baitu. Tuvākajā nākotnē paredzams,
ka viņi pārspriedīs tādu datoru cenas, kuru operāciju
skaits sekundē izteiksies ar triljoniem.
Ļoti lielas un ļoti
mazas kvantitātes
Pavisam citāda ir mūsdienu fiziķu un
astronomu ikdiena. Viņi operē gan ar ļoti lieliem, gan ar
ļoti maziem skaitļiem, lai izteiktu tās kvantitātes, kuras
nozīmīgas šo zinātņu teorijai un praksei. Astronomi
spiesti aplūkot milzīgus attālumus, gigantiskas masas un
neiedomājamas intensitātes gravitācijas laukus; fiziķi
pēta niecīga izmēra elementārdaļiņas,
ārkārtīgi augstas frekvences elektromagnētiskās
svārstības un milzīgus enerģētiskos procesus.
Zvaigžņu attālumi mūsu galaktikā ir tik milzīgi,
ka izteikt tos kilometros nav ērti, tāpēc tiek izmantotas
tādas mērvienības kā gaismas gadi (ly) un parseki (pc).
Viens gaismas gads ir attālums, kuru gaisma vakuumā noskrien gada
laikā, bet parseks ir tāds debess ķermeņa attālums no
mūsu saules sistēmas, kura gada paralakse ir 1 sekunde. Kilometros
šīs mērvienības izsakāmas ar šādām
sakarībām: 1 ly = 9,4605*1012km, 1 pc = 3,0856*1013 km.
Tātad šīs astronomiskās
mērvienības izsakāmas ar kilometru triljoniem. Fiziķi ar
līdzīgiem skaitļiem saduras, aplūkojot t. s. cietos
(rentgena un gamma) elektromagnētiskos starojumus. Gamma starojuma
viļņu garums l
izsakāms kā nanometra desmitdaļa (1nm = 10-9m), bet
šī starojuma frekvence h izteiksies ar skaitli 3*1015, t. i., h = 3 kvadriljoni
svārstību sekundē.
Kā ļoti mazas, tā arī ļoti
lielas kvantitātes sevī slēpj gan teorētiskas, gan arī
praktiskas problēmas. Ģeniālais vācu matemātiķis
Bernhards Rīmanis (1826.1866.) izteica domu, ka ģeometrijas
pamatprincipi ļoti mazos telpiskos apgabalos ir atšķirīgi
no tiem, kādi pastāv ļoti lielos. Slavenais krievu ģeometrs
Nikolajs Lobačevskis (1792.1856.) savas neeiklīda ģeometrijas
attaisnojumu meklēja astronomiskajā telpā, t. i., lielo
attālumu pasaulē. Šodien lielie attālumi mūsu
uzmanību var piesaistīt no sakaru tehnikas viedokļa.
Pēdējos gadu desmitos astronomi
atklājuši, ka mūsu galaktikā ir desmitiem
zvaigžņu, ap kurām riņķo planētas. Tātad
pastāv iespēja, ka mūsu galaktikas ietvaros Zeme nav
vienīgā planēta, uz kuras mājo saprātīgas
būtnes. Nākotnē mums tātad var rasties iespēja
stāties kontaktos ar citplanētiešiem. Tā kā mūsu
saules sistēmas planētas, izņemot Zemi, maz piemērotas
augsti attīstītu būtņu attīstībai un eksistencei,
tad šie citplanētieši varētu būt meklējami tikai
uz citu sauļu, citu zvaigžņu planētām. Taču
attālumi līdz tām izsakāmi ar parseku desmitiem. Ja
pieņemtu, ka šādas zvaigznes, resp., planētas,
attālumi līdz mūsu Zemei ir 20 pc, tad varam iztēloties,
kā notiks mūsu kontaktēšanās ar šīs
tālās zvaigznes citplanētiešiem. Jautājumi, kurus
adresēsim šīm būtnēm, pie tām nonāks tikai
pēc 65 gadiem, jo radioviļņu izplatības ātrums nav
lielāks par gaismas ātrumu, t. i., nepārsniedz 300 000 km/s. Bet
20 parseki atbilst 65,23 gaismas gadiem. Tātad atbildi no viņiem (pats
ātrākais) varam saņemt pēc 130 gadiem, kad jautājumu
sūtītāji droši vien būs miruši.
Vai iespējami kādi sakaru veidi, kuri
ļautu kontaktēties ar citplanētiešiem īsākā
laika sprīdī? Uz to negatīvu atbildi dod modernā
relativitātes teorija, kura postulē, ka jebkura signāla
izplatīšanas ātrums nevar pārsniegt gaismas ātrumu.
Taču tagad divi krievu zinātnieki, G. Šipovs un A. Akimovs,
reklamē jaunu fizikālu teoriju, kura noliedz minēto
relativitātes teorijas postulātu. Viņi uzskata, ka
iespējams konstruēt t. s. torsionu ģeneratorus, kuri ļautu
informācijas signālus parraidīt ar neierobežotu
ātrumu. Latvijā šos uzskatus propagandē
akadēmiķis A. Buiķis. Tomēr jāatzīmē, ka
torsionu teorijas secinājumi nevienā eksaktā fizikālā
eksperimentā nav apstiprināti, un nopietni fiziķi pret G. Šipova
jauno fizikālo teoriju izturas ar pamatotu skepsi.
Maģiskie skaitļi
Joprojām ir ne mazums cilvēku, kuri noteiktiem
skaitļiem piedēvē maģisku nozīmi. Piemēram,
skaitlis 13 jeb t. s. velna ducis tiek apveltīts ar ļaunuma
auru; skaitlis 666 jeb tā sauktais zvēra skaitlis tiek
uzskatīts par sātana kodu, un tam līdz pat šai dienai tiek
meklēts skaidrojums reliģiskos traktātos. Bīstami ir
arī pārskaitļi. Jubilāram dāvināmo ziedu
nedrīkst būt pārskaitlis, tas pieļaujams bēru
ceremonijās nolikto ziedu skaitam. Pārskaitlis neder arī
zīlēšanai pēc ziedlapiņām, jo mīl nemīl
pārskaitļa gadījumā beigsies ar nemīl.
Savukārt skaitlim 7 tiek piedēvēta labu vēstoša
nozīme.
Lai gan šādai skaitļu
mistifikācijai nav atrodams racionāls pamats, tā stabili
saglabājusies cauri gadsimtiem. Pārskaitļus jau senie
grieķi uzskatīja par sabrukšanas, sadalīšanās reprezentantiem,
jo tie taču dalās ar divi. Zvēra skaitļa 666 izcelsme
saistās ar Jāņa atklāsmes grāmatas jeb Apokalipsis
sarakstīšanas laiku, t.i., mūsu ēras 1. gs. Kur
meklējama velna duča sākotne, autoram nav zināms.
Skaitļu psiholoģiskā
nozīme
Reklāmu devēji bieži spekulē uz
sabiedrības kvantitatīvās izglītības zemo līmeni.
Tā, piemēram, bankas aicina izdarīt depozitāros
noguldījumus ar norādi, ka tieši šajā bankā
jūs saņemsiet paaugstinātus noguldījumu procentus. Tas
klienta ausīm skan ļoti pievilcīgi. Taču īstenībā
jūs saņemsiet procentu likmes pazeminājumu, ja to
salīdzināsiet ar iepriekšējo gadu vai kādas citas
bankas piedāvājumu. Melots nav, jo reklāmā nav
norādīts, ar ko jāsalīdzina šīs procentu likmes
palielinājums. Lielveikali nereti aicina pircējus uz sezonas
noslēguma akciju, deklarējot, ka gandrīz visām (varbūt
arī visām precēm) cenas pazeminātas līdz pat 50
procentiem. Šajā gadījumā varat būt drošs, ka
vērtīgākajām precēm šis pazeminājums
būs vismazākais. Autors par to pārliecinājās,
apmeklējot universālveikals Centrs.
Latvijas Radio 1 atkārtoti pārraida
lielveikalu tīkla reklāmu: Drogas garantē
zemākās cenas. Kārtējo reizi tiek noklusēti tie
nosacījumi, pie kuriem klients var izteikt pretenzijas, ja kādā
citā veikalā tām pašām precēm cena būs
vēl zemāka. Par to pārliecinājusies žurnāliste
Sigita Treibere no avīzes Vakara Ziņas.
Banka Baltija savulaik piesaistīja
noguldītājus, solot (un arī izmaksājot) augstus
noguldījumu procentus, kas sākuma periodā sasniedza pat 90
procentu likmi. Kādreizējā Finanšu ministrijas darbiniece
Inguna Sudraba šīs bankas klientiem vēlāk pārmeta
iedzīvošanās kāri. Šinī gadījumā
noklusēts tika svarīgs kvantitatīvs rādītājs
inflācijas līmenis, kurš toreiz pārsniedza 100 procentus
gadā, t. i., ka preču cenas Latvijas Republikā gada laikā
dubultojās. Tātad noguldītājs gada beigās kopā ar
noguldījuma procentiem saņēma mazāk, nekā bija
noguldījis. Tātad lieliska iedzīvošanās!
Varbūt subjektīvi dažs labs klients cerēja uz savu
ienākumu palielinājumu, taču praksē katrs redzēja
realitāti pat bez īpašas rēķināšanas.
Mērāmas un
nemērāmas kvantitātes
Mūsos attīstījusies stabila tendence
visu mērīt, visu izteikt kvantitatīvi ar skaitļu un
mērskaitļu palīdzību. Bijuši arī
mēģinājumi mērīt skaistumu. Tomēr ne visas
parādības izsakāmas ar eksaktiem raksturlielumiem. Kritiski
vērtējami arī tādi kvantitatīvie raksturlielumi
kā intelekta koeficients (IQ) un inflācijas gada procents. Šo
rādītāju izskaitļošana balstīta uz tādu faktoru
kompleksa izmantošanu, kuriem ir samērā relatīvs raksturs,
līdz ar to attiecīgo rādītāju interpretācija ir
diezgan problemātiska. Ko, piemēram, konkrētai namamātei
izsaka ekonomistu publicētais paziņojums, ka inflācijas
līmenis Latvijā sasniedzis 7 procentus? Vai tad visām
precēm, kuras interesē šo namamāti, cenas
palielinājušās par septiņiem procentiem? Nekā
tamlīdzīga!
Jā, mūsu vēlmēm visu
mērīt gan ir savas robežas, taču tādēļ
nedrīkst kultivēt praksi aizstāt eksaktus raksturlielumus ar
tāda veida kategoriāliem apgalvojumiem un paziņojumiem, kuri
maskē parādību būtību. Tādas frāzes kā Latvijas
iestājai ES bija liels sabiedrības atbalsts, Baltijas
jūra ir ļoti piesārņota, televīzijas
skatītāju nospiedošs vairākums atbalstīja Sandras
Kalnietes kandidatūru lielā mērā maskē patieso
realitāti, un plašsaziņas līdzekļos tās
varētu figurēt tikai kā apkopojoši secinājumi, kuri
izriet no precīziem kvantitatīviem rādītājiem.
prof. Aivars LORENCS
Par mūsu sabiedrības visai apšaubāmo kvantitatīvās izglītības līmeni (ang. quantitative literacy) liecina ciparu vīrusa plašā izplatība politiķu, žurnālistu, ierēdņu un pat dažu zinātnieku leksikā. Šķiet, ka pirmais šo vīrusu apgrozībā palaida Aivars Guntis Kreituss.
Ciparu vīruss
Tas izrādījās tik virulents, ka tagad būs grūti atrast žurnālistu vai politiķi, kurš ar to nebūtu inficēts. Firmu investīciju apjomi tiek ilustrēti ar cipariem, darba vietu skaits tiek dēvēts par ciparu. Uzņēmuma peļņa izteikta ar tiem vai citiem cipariem utt. Latviešu valodas vārds skaitlis tiek padzīts no mūsu leksikas un aizstāts ar ciparu. Tādēļ nebūs lieki atgādināt, ka decimālajā skaitīšanas sistēmā mēs lietojam desmit arābu ciparus 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, bet binārajā tikai divus 0, 1.
Vieni un tie paši cipari dažādā sakārtojumā apzīmē atšķirīgus skaitļus, kuru vienādošana vienādo ciparu dēļ ne ar ko nav attaisnojama. Pavisam smieklīgi skan apgalvojums, ka cipars 521 ir lielāks par ciparu 125. Tikpat dīvaini skan apgalvojums, ka zinātnei atvēlētais valsts budžeta cipars 0,2 procenti no iekšzemes kopprodukta turpmākajos gados jāpaaugstina, lai sasniegtu 1 procentu.
Mērskaitļu dīvainības
Gan ikdienā, gan zinātnē operējam ar kvantitātēm, kuras interpretējamas kā zināmu lielumu salīdzinājumi ar noteiktiem etaloniem mērvienībām. Zemes platības tiek izteiktas hektāros vai kvadrātkilometros, ķermeņa masa gramos, kilogramos vai tonnās. Elektrisko strāvu spriegumi voltos vai kilovoltos utt. Lai pareizi operētu ar mērskaitļiem, precīzi jāievēro etalonu, t. i., izmantoto mērvienību savstarpējās attiecības. Īpaši uzmanīgam jābūt ar mērvienībām, kuras nepieder metriskajai sistēmai. Spilgtu liecību par tulkotāju un redaktoru kvantitatīvās izglītības līmeni sniedz Žila Verna grāmatā Žangada sastopamie elektrisko zušu un skudrulāču raksturlielumi. Tur lasāms, ka elektrisko zušu garums sasniedzot 20 pēdas, platums 8 sprīžus, skudrulāču nagu garums 5 sprīžus.
Rodas jautājums, kādi ir šo dzīvo būtņu izmēri metriskajās vienībās? Ja ar pēdu domāta angļu pēda (foot), tad mums būs darīšana ar gigantiskiem radījumiem, kuru garums svārstās no 4,5 līdz 6 metriem. Neskaidrs paliek jautājums par elektrisko zušu platumu un skudrulāču nagu garumu. Franču mēra sistēmā tāda mērvienība kā sprīdis nav atrodama, tas pats sakāms par angļu mēriem. Ja ar sprīdi saprotam pieauguša cilvēka sprīža vidējo garumu, tad šis etalons nebūs mazāks par 15 cm. Tātad elektrisko zušu platums nebūs mazāks par 1,2 m, bet skudrulāča nagu garums sasniegs 75 cm. Jāšaubās, vai Žils Verns būtu paudis šādas zooloģiskas aplamības. Tas izskaidrojams ar grāmatas tulkotājas Mirdzas Ersas kvantitatīvās izglītības trūkumiem.
Par kvantitatīvās izglītības kuriozu jānosauc grāmatas Atveseļojies pats! sastādītājas un redaktores T. Laubes rekomendācija kāda ārstnieciska preparāta sagatavošanai. Lasītājam tiek dots norādījums izšķīdināt 8 g medus 8 mg ūdens! Šajā pašā darbā jauktas tādas mērvienības kā dekalitri un decilitri, lasāmas arī citas dīvainības.
Ar daudz sarežģītāku kvantitatīvās izglītības problēmu saduramies jautājumos, kas attiecas uz sakaru tehnikas un informācijas drošības jautājumiem. Šeit nereti gadās, ka eksaktas mērvienības objektīvi nav iespējamas, bet vienlaikus pastāv nepieciešamība kādas kvantitatīvas noteiksmes salīdzināt, t. i., tās kaut kādā veidā mērīt. Spilgts piemērs tam ir elektroniskā paraksta drošums.
Ja apgalvo, ka Latvijā tiks ieviests drošs elektroniskais paraksts, tad lasītājam var rasties iespaids, ka šī paraksta drošība ir kas absolūts. Faktiski drošs elektroniskais paraksts tomēr ir apveltīts ar noteiktu nedrošības līmeni, jo tā viltošana (ang. forgery) tāpat ir iespējama. Tātad rodas jautājums, cik īsti drošs, resp., nedrošs, būs mūsu elektroniskais paraksts? Mēs prasām pēc kāda kvantitatīva rādītāja, kas šo drošības līmeni izteiktu.
Nedaudz vienkāršojot situāciju, varam teikt, ka drošības kvantitatīvais rādītājs ir elementāro aritmētisko operāciju skaits, kas nepieciešams, lai izskaitļotu, t.i., atrastu, nezināma elektroniskā paraksta atslēgu jeb paraksta veidošanas algoritmu. Ja nepieciešamo operāciju skaits šāda mērķa sasniegšanai būtu 1 sekstiljons, t. i., 1021, tad vismodernākajam datoram būtu jāpatērē vismaz 30 gadi, lai šo uzdevumu veiktu. Šis aprēķins balstās uz pieņēmumu, ka šodien tiek konstruēti datori, kuru darbības ātrums būs triljons aritmētisku operāciju sekundē. Tā kā sekunžu skaits vienā gadā nav lielāks par 32 miljoniem, tad gada laikā šāds dators izpildīs 3,2*1019 operācijas. Dalot 1021 ar 3,2*1019, dabūsim 31,25, kas izsaka nepieciešamo gadu skaitu.
Mūsu atbilde tomēr rāda, cik relatīvs ir šāds augstas drošības rādītājs. Atliek tikai pacelt datora ātrdarbību par vienu vai divām kārtām, un drošais elektroniskais paraksts kļūs ārkārtīgi nedrošs.
Kvantitātes un skaitļi
Mūsu izpratne par kvantitātēm, par lielumiem primāri balstās uz jēdzienu skaits, kas abstrahēts no mūsu pieredzes, darbojoties ar viendabīgu priekšmetu kopām, t. i., skaitot lopus ganāmpulkā, bērnus ģimenē, zvērādas noliktavā, karotāju skaitu ciltij utt. Tā nonāca pie jēdziena naturāls skailtis jeb dabisks skaitlis. Decimālajā skaitīšanas sistēmā tos pierakstām ar jau pieminētajiem desmit arābu cipariem, bet binārajā jeb diviskajā skaitīšanas sistēmā ar cipariem 0 un 1. Naturālo skaitļu fundamentālo nozīmi ievērojamais vācu matemātiķis Leopolds Kronekers (1823.1891.) izteica ar šādu sentenci: - Dievs radīja naturālos skaitļus, pārējais ir cilvēku roku darbs.
Nākošā pakāpe mūsu
izpratnē par kvantitātēm saistās ar naturālo
skaitļu attiecībām jeb t. s. racionālajiem skaitļiem:
½, 1/3, ¼, 1/5, 2/3, 2/4, 3/5 utt. Grieķi vairākus
gadsimtus pirms mūsu ēras atklāja, ka dažu lielumu izteikšanai
arī racionālie skaitļi ir nepietiekami. Viņi
pierādīja, ka kvadrāta malas attiecība pret tā diagonāli
nav izsakāma ar racionālu skaitli, t. i., ar divu naturālu
skaitļu m un n attiecību m/n. Ja kvadrāta malas garums ir 1m,
tad tā diagonāles garums būs![]() m. Tātad šo divu
nogriežņu garumu attiecība būs
m. Tātad šo divu
nogriežņu garumu attiecība būs ![]() , kur
, kur ![]() ir irracionāls skaitlis, kas
pierakstāms kā bezgalīga, nepereodiska decimāldaļa.
ir irracionāls skaitlis, kas
pierakstāms kā bezgalīga, nepereodiska decimāldaļa.
Tagad skaitļa jēdziens ar daudzu matemātiķu pūlēm paplašināts līdz t. s. kompleksajiem skaitļiem, kuru loma modernajā zinātnē nav pārvērtējama. Ikdienā cilvēki iztiek ar naturāliem un racionāliem skaitļiem, pēdējos visbiežāk pierakstot decimālskaitļu formā. Pēc lieluma šie skaitļi reti kad pārsniedz miljardu un tikpat reti to vērtība mazāka par vienu miljardo daļu, t. i, 1/10000000000. Taču pašreizējā ikdiena būtiski atšķiras no ikdienas pagātnē. Senie grieķi praktiskās lietas kārtoja tādu kvantitāšu ietvaros, kuru mērskaitļi atradās robežās starp 1/1000 un 1000; nulli viņi par skaitli neuzskatīja. Skaitli 10 000 grieķi apzīmēja ar vārdu miriāde. Tas viņiem šķita tik milzīgs, ka drīz vien ar to apzīmēja kaut ko neskaitāmu. Tā, piemēram, sāka runāt par zvaigžņu miriādēm, par kukaiņu miriādēm u. tml. Arī senajā Krievzemē, runājot par skaitu, kas izsakāms ar 10 000, lietoja izteiksmīgu vārdu tumsa (kr. ņüģą). Bet jau 17. gs. ņüģą apzīmēja miljonu. Tehnoloģijas attīstība cilvēkus spiež arī ikdienā lietot arvien lielākus un lielākus skaitļus. Mūsdienu jaunieši jau runā par diskiem, kuru kapacitāte izsakāma gigabaitos, t. i., miljardos baitu. Tuvākajā nākotnē paredzams, ka viņi pārspriedīs tādu datoru cenas, kuru operāciju skaits sekundē izteiksies ar triljoniem.
Ļoti lielas un ļoti mazas kvantitātes
Pavisam citāda ir mūsdienu fiziķu un astronomu ikdiena. Viņi operē gan ar ļoti lieliem, gan ar ļoti maziem skaitļiem, lai izteiktu tās kvantitātes, kuras nozīmīgas šo zinātņu teorijai un praksei. Astronomi spiesti aplūkot milzīgus attālumus, gigantiskas masas un neiedomājamas intensitātes gravitācijas laukus; fiziķi pēta niecīga izmēra elementārdaļiņas, ārkārtīgi augstas frekvences elektromagnētiskās svārstības un milzīgus enerģētiskos procesus. Zvaigžņu attālumi mūsu galaktikā ir tik milzīgi, ka izteikt tos kilometros nav ērti, tāpēc tiek izmantotas tādas mērvienības kā gaismas gadi (ly) un parseki (pc). Viens gaismas gads ir attālums, kuru gaisma vakuumā noskrien gada laikā, bet parseks ir tāds debess ķermeņa attālums no mūsu saules sistēmas, kura gada paralakse ir 1 sekunde. Kilometros šīs mērvienības izsakāmas ar šādām sakarībām: 1 ly = 9,4605*1012km, 1 pc = 3,0856*1013 km.
Tātad šīs astronomiskās mērvienības izsakāmas ar kilometru triljoniem. Fiziķi ar līdzīgiem skaitļiem saduras, aplūkojot t. s. cietos (rentgena un gamma) elektromagnētiskos starojumus. Gamma starojuma viļņu garums l izsakāms kā nanometra desmitdaļa (1nm = 10-9m), bet šī starojuma frekvence h izteiksies ar skaitli 3*1015, t. i., h = 3 kvadriljoni svārstību sekundē.
Kā ļoti mazas, tā arī ļoti lielas kvantitātes sevī slēpj gan teorētiskas, gan arī praktiskas problēmas. Ģeniālais vācu matemātiķis Bernhards Rīmanis (1826.1866.) izteica domu, ka ģeometrijas pamatprincipi ļoti mazos telpiskos apgabalos ir atšķirīgi no tiem, kādi pastāv ļoti lielos. Slavenais krievu ģeometrs Nikolajs Lobačevskis (1792.1856.) savas neeiklīda ģeometrijas attaisnojumu meklēja astronomiskajā telpā, t. i., lielo attālumu pasaulē. Šodien lielie attālumi mūsu uzmanību var piesaistīt no sakaru tehnikas viedokļa.
Pēdējos gadu desmitos astronomi atklājuši, ka mūsu galaktikā ir desmitiem zvaigžņu, ap kurām riņķo planētas. Tātad pastāv iespēja, ka mūsu galaktikas ietvaros Zeme nav vienīgā planēta, uz kuras mājo saprātīgas būtnes. Nākotnē mums tātad var rasties iespēja stāties kontaktos ar citplanētiešiem. Tā kā mūsu saules sistēmas planētas, izņemot Zemi, maz piemērotas augsti attīstītu būtņu attīstībai un eksistencei, tad šie citplanētieši varētu būt meklējami tikai uz citu sauļu, citu zvaigžņu planētām. Taču attālumi līdz tām izsakāmi ar parseku desmitiem. Ja pieņemtu, ka šādas zvaigznes, resp., planētas, attālumi līdz mūsu Zemei ir 20 pc, tad varam iztēloties, kā notiks mūsu kontaktēšanās ar šīs tālās zvaigznes citplanētiešiem. Jautājumi, kurus adresēsim šīm būtnēm, pie tām nonāks tikai pēc 65 gadiem, jo radioviļņu izplatības ātrums nav lielāks par gaismas ātrumu, t. i., nepārsniedz 300 000 km/s. Bet 20 parseki atbilst 65,23 gaismas gadiem. Tātad atbildi no viņiem (pats ātrākais) varam saņemt pēc 130 gadiem, kad jautājumu sūtītāji droši vien būs miruši.
Vai iespējami kādi sakaru veidi, kuri ļautu kontaktēties ar citplanētiešiem īsākā laika sprīdī? Uz to negatīvu atbildi dod modernā relativitātes teorija, kura postulē, ka jebkura signāla izplatīšanas ātrums nevar pārsniegt gaismas ātrumu. Taču tagad divi krievu zinātnieki, G. Šipovs un A. Akimovs, reklamē jaunu fizikālu teoriju, kura noliedz minēto relativitātes teorijas postulātu. Viņi uzskata, ka iespējams konstruēt t. s. torsionu ģeneratorus, kuri ļautu informācijas signālus parraidīt ar neierobežotu ātrumu. Latvijā šos uzskatus propagandē akadēmiķis A. Buiķis. Tomēr jāatzīmē, ka torsionu teorijas secinājumi nevienā eksaktā fizikālā eksperimentā nav apstiprināti, un nopietni fiziķi pret G. Šipova jauno fizikālo teoriju izturas ar pamatotu skepsi.
Maģiskie skaitļi
Joprojām ir ne mazums cilvēku, kuri noteiktiem skaitļiem piedēvē maģisku nozīmi. Piemēram, skaitlis 13 jeb t. s. velna ducis tiek apveltīts ar ļaunuma auru; skaitlis 666 jeb tā sauktais zvēra skaitlis tiek uzskatīts par sātana kodu, un tam līdz pat šai dienai tiek meklēts skaidrojums reliģiskos traktātos. Bīstami ir arī pārskaitļi. Jubilāram dāvināmo ziedu nedrīkst būt pārskaitlis, tas pieļaujams bēru ceremonijās nolikto ziedu skaitam. Pārskaitlis neder arī zīlēšanai pēc ziedlapiņām, jo mīl nemīl pārskaitļa gadījumā beigsies ar nemīl. Savukārt skaitlim 7 tiek piedēvēta labu vēstoša nozīme.
Lai gan šādai skaitļu mistifikācijai nav atrodams racionāls pamats, tā stabili saglabājusies cauri gadsimtiem. Pārskaitļus jau senie grieķi uzskatīja par sabrukšanas, sadalīšanās reprezentantiem, jo tie taču dalās ar divi. Zvēra skaitļa 666 izcelsme saistās ar Jāņa atklāsmes grāmatas jeb Apokalipsis sarakstīšanas laiku, t.i., mūsu ēras 1. gs. Kur meklējama velna duča sākotne, autoram nav zināms.
Skaitļu psiholoģiskā nozīme
Reklāmu devēji bieži spekulē uz sabiedrības kvantitatīvās izglītības zemo līmeni. Tā, piemēram, bankas aicina izdarīt depozitāros noguldījumus ar norādi, ka tieši šajā bankā jūs saņemsiet paaugstinātus noguldījumu procentus. Tas klienta ausīm skan ļoti pievilcīgi. Taču īstenībā jūs saņemsiet procentu likmes pazeminājumu, ja to salīdzināsiet ar iepriekšējo gadu vai kādas citas bankas piedāvājumu. Melots nav, jo reklāmā nav norādīts, ar ko jāsalīdzina šīs procentu likmes palielinājums. Lielveikali nereti aicina pircējus uz sezonas noslēguma akciju, deklarējot, ka gandrīz visām (varbūt arī visām precēm) cenas pazeminātas līdz pat 50 procentiem. Šajā gadījumā varat būt drošs, ka vērtīgākajām precēm šis pazeminājums būs vismazākais. Autors par to pārliecinājās, apmeklējot universālveikals Centrs.
Latvijas Radio 1 atkārtoti pārraida lielveikalu tīkla reklāmu: Drogas garantē zemākās cenas. Kārtējo reizi tiek noklusēti tie nosacījumi, pie kuriem klients var izteikt pretenzijas, ja kādā citā veikalā tām pašām precēm cena būs vēl zemāka. Par to pārliecinājusies žurnāliste Sigita Treibere no avīzes Vakara Ziņas.
Banka Baltija savulaik piesaistīja noguldītājus, solot (un arī izmaksājot) augstus noguldījumu procentus, kas sākuma periodā sasniedza pat 90 procentu likmi. Kādreizējā Finanšu ministrijas darbiniece Inguna Sudraba šīs bankas klientiem vēlāk pārmeta iedzīvošanās kāri. Šinī gadījumā noklusēts tika svarīgs kvantitatīvs rādītājs inflācijas līmenis, kurš toreiz pārsniedza 100 procentus gadā, t. i., ka preču cenas Latvijas Republikā gada laikā dubultojās. Tātad noguldītājs gada beigās kopā ar noguldījuma procentiem saņēma mazāk, nekā bija noguldījis. Tātad lieliska iedzīvošanās! Varbūt subjektīvi dažs labs klients cerēja uz savu ienākumu palielinājumu, taču praksē katrs redzēja realitāti pat bez īpašas rēķināšanas.
Mērāmas un nemērāmas kvantitātes
Mūsos attīstījusies stabila tendence visu mērīt, visu izteikt kvantitatīvi ar skaitļu un mērskaitļu palīdzību. Bijuši arī mēģinājumi mērīt skaistumu. Tomēr ne visas parādības izsakāmas ar eksaktiem raksturlielumiem. Kritiski vērtējami arī tādi kvantitatīvie raksturlielumi kā intelekta koeficients (IQ) un inflācijas gada procents. Šo rādītāju izskaitļošana balstīta uz tādu faktoru kompleksa izmantošanu, kuriem ir samērā relatīvs raksturs, līdz ar to attiecīgo rādītāju interpretācija ir diezgan problemātiska. Ko, piemēram, konkrētai namamātei izsaka ekonomistu publicētais paziņojums, ka inflācijas līmenis Latvijā sasniedzis 7 procentus? Vai tad visām precēm, kuras interesē šo namamāti, cenas palielinājušās par septiņiem procentiem? Nekā tamlīdzīga!
Jā, mūsu vēlmēm visu mērīt gan ir savas robežas, taču tādēļ nedrīkst kultivēt praksi aizstāt eksaktus raksturlielumus ar tāda veida kategoriāliem apgalvojumiem un paziņojumiem, kuri maskē parādību būtību. Tādas frāzes kā Latvijas iestājai ES bija liels sabiedrības atbalsts, Baltijas jūra ir ļoti piesārņota, televīzijas skatītāju nospiedošs vairākums atbalstīja Sandras Kalnietes kandidatūru lielā mērā maskē patieso realitāti, un plašsaziņas līdzekļos tās varētu figurēt tikai kā apkopojoši secinājumi, kuri izriet no precīziem kvantitatīviem rādītājiem.
prof. Aivars LORENCS

